math authentique

Des exercices supplémentaires sur le parallélogramme.

    A mathematician once asked the following question to a group of students from several countries: how do you write 4 in between 5? The answers were as follows: From China: is his a joke? From Japan: impossible! From USA: the question is wrong. From England: it’s absurd. From Lebanon: it’s so simple habibi, F IV E.

Presque tout le monde sait la règle de la multiplication d’un nombre par 10 c’est ajouter 0 a ce nombre ex :                     4 × 10=40                   51 × 10=510                 238 × 10=2380 Mais peu de personne sache comment on multiplie par 11 pour cela je l’explique pour vous. Un nombre d’un seul chiffre multiplié par 11 ex : 3×11=33. Un nombre de deux chiffres multipliés par 11 ex : 26×11=286                       47×11=517 3. Lorsque on multiple un nombre contenant au moins 3 chiffres ex : 356×11=3916 567×11=6237

J’ai préparé des exercices de révision sur la racine carre.

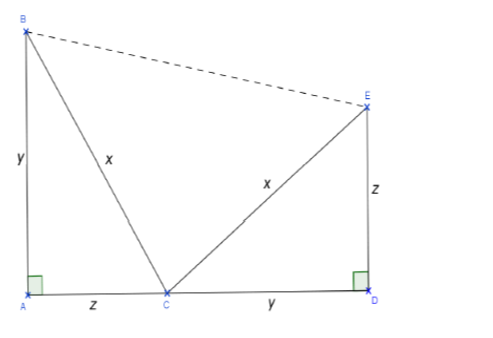
     Je mets en votre disposition une activité qui sert à démontrer  le théorème de Pythagore par une  méthode facile.     L’activité :     ABC est un triangle rectangle en A tel que BC = x, AB = y et AC = z. On place sur la demi droite [AC) le point D tel que DC= y du point D on mène la droite perpendiculaire a (AC) sur cette droite on place le point E tel que DE=z.     Comme la montre la figure ci-dessous.     Tu peux utiliser les informations suivantes sans démonstration : ADEB trapèze, BCE triangle rectangle en C, EC=x. 1.     En additionnant l’aire des trois triangles, montrer que l’aire du trapèze ABED est égal à x 2 /2 +xy 2.     En appliquant la formule de l’aire du trapèze ( A= (petite base +grande base )/2 ×hauteur),          Montrer que l’aire du trapèze ABED est égale à y 2 /2+z 2 /2+xy. 3.      En déduire la relation de Pythagore : BC 2 =AB 2 +AC 2 .

Did you ever wonder what is the origin of the radical sign? The radical is long been used in the world The oldest proof of usage of square root is this artefact found in today Iraq and it shows radical of 2      Many scholars believes it was originated from the deformation of letter “r” the first letter of radical but other believes it is a deformation of the Arabic letter” ج ” which is the first letter of the Arabic word” جذر ”that means root in Arabic , the symbol was written like this √ 2   or √5.    

السلام عليكم. سوف اذكر لكم بعض المسائل التي عرضت على الامام علي(ع) وأجاب عنها اتمنى ان يستفاد منها لتعزيز حب التلاميذ لمادة الرياضيات و ربط هذه المادة بالحياة الواقعية قديماً وحديثاً.قراءة ممتعة. سوف يتم تحديث هذه المدونة عند اضطلاعي على أي مسألة لم أذكرها. وأتمنى لفت انتباهي الى مسائل لم أذكرها وشكراً. ﺍﻟﻤﺴﺄﻟﺔ الاولى:        ﺟﺎء إﻟﻰ  الامام ﻋﻠﻲّ(ع ) ﺛﻼﺛﺔ رﺟﺎل ﯾﺨﺘﺼﻤﻮن ﻓﻲ ﺳﺒﻌﺔ ﻋﺸﺮ ﺟﻤﻼ ،ﻓﻘﺎﻟﻮا له إن ﻷﺣﺪﻧﺎ ﻧﺼﻔﮭﺎ وﻟﻶﺧﺮ ﺛﻠﺜﮭﺎ وﻟﺜﺎﻟﺜﻨﺎ ﺗﺴﻌﮭﺎ وﻧﺮﯾﺪ أن ﺗﻘﺴﻤﮭﺎ ﺑﯿﻨﻨﺎ  ﻋﻠﻰ أن ﻻ  ﯾﺒﻘﻰ ﻣﻨﮭﺎ ﺑﺎق.      ﻓﻘﺎل ﻋﻠﻲ(ع )  أﺗﺮﺿﻮن أن أﺿﻊ ﻣﻨﻲ ﺟﻤﻼ ﻓﻮﻗﮭﺎ واﻗﺴﻤﮭﺎ ﺑﯿﻨﻜﻢ ﻓﻘﺎﻟﻮا ﻧﻌﻢ .  ﻓﻮﺿﻊ ﻋﻠﻲ (ع )   واﺣﺪا ﻓﻮﻗﮭﺎ ﻓﺼﺎرت ﺛﻤﺎﻧﯿﺔ ﻋﺸﺮ ﺟﻤﻼ ﻓﺄﻋﻄﻰ اﻷول ﻧﺼﻔﮭﺎ أي ﺗﺴﻌﺔ ﺟﻤﺎل وھﻮ ﻧﺼﻒ اﻟﺜﻤﺎﻧﯿﺔ ﻋﺸﺮ ﺟﻤﻼ وأﻋﻄﻰ اﻟﺜﺎﻧﻲ ﺛﻠﺜﮭﺎ أي ﺳﺘﺔ ﺟﻤﺎل وهو ﺛﻠﺚ اﻟﺜﻤﺎﻧﯿﺔ ﻋﺸﺮ ﺟﻤﻼ وأﻋﻄﻰ اﻟﺜﺎﻟﺚ ﺗﺴﻌﮭﺎ أي ﺟﻤﻠﯿﻦ وھﻮ ﺗﺴﻊ اﻟﺜﻤﺎﻧﯿﺔ ﻋﺸﺮ ﺟﻤﻼ ﻓﺄﺻﺒﺢ ﻣﺠﻤﻮع ﻣﺎ أﻋﻄﻰ ﻟﮭﻢ ﻣﻦ اﻟﺠﻤﺎل ﺳﺒﻌﺔ ﻋﺸﺮ ﺟﻤﻼ، وهو  ﻣﺠﻤﻮع اﻟﺘﺴﻌﺔ ﻣﻊ اﻟﺴﺘﺔ ﻣﻊ اﻻﺛﻨﯿﻦ وﺑﻘﻲ ﻣﻦ اﻟﺜﻤﺎﻧﯿﺔ ﻋﺸﺮ ﺟﻤﻼ ﺟﻤﻞ واﺣﺪ  وھﻮ ﺟﻤله (ع ) اﻟﺬي أﺿﺎفه إﻟﻰ ﺟﻤﺎﻟﮭﻢ ﻗﺒﻞ اﻟﻘﺴﻤﺔ.     وﺑﺬﻟﻚ ﻓﻘﺪ ﻗﺴﻢ اﻹﻣﺎم ﻋﻠﻲّ(ع

  Bonjour, j'ai fait des activités sur les identités remarquable pour que vous mieux comprendre les identités remarquables.   Vous aller suivre les consignes dans les activités et les résoudre enfin vous constatera vous-même les identités suivants (remarque le forme factorisé est avant l’égalité et la forme développé est après l’égalité): (a+b) 2 =a 2 +2ab+b 2 (a-b) 2 =a 2 -2ab+b 2 (a+b)(a-b) =a 2 -b 2    J’espère ça va être utile pour vous.

    L’idée des chiffres était d’origine indien cet idée est arrivé au pays arabe ou ils sont  ils sont utilisés ces chiffres,  le  mathématicien   Al-Khawarizmi a inventé le zéro et les formes suivants mais le reste des pays arabes surtout les pays asiatiques ils sont adoptes des  déformations  des chiffres indiens originals.     Les chiffres arabes sont conçus en fonction du nombre d'angles pour chaque nombre, comme suit: Le chiffre   un... Un angle Le chiffre deux... Deux angles Le chiffre trois… Trois angles Le chiffre   quatre... Quatre angles Le chiffre cinq ... Cinq angles Le chiffre   six ... Six angles Le chiffre   sept … Sept angles Le chiffre est huit… Huit angles Le chiffre   neuf   ... Neuf angles Et enfin le chiffre   zéro... Pas d'angle     Et puis ils ont fait des modifications sur ces formes, jusqu’à ce qu’ils sont devenus les formes actuellement connues.     Ces chiffres sont  introduits en Europe par les Arabes au 10e si

Comme je vous avais promis. Je partage avec vous une représentation   power point sur le chapitre racine carrée en espérant que ça vous aide à mieux comprendre ce chapitre. N’hésitez pas de commenter sur cette représentation et de partager vos remarques avec moi. Vous êtes libre de faire ce que vous veule par cette représentation. Racine Carre.alaa by on Scribd

J’ai trouvé que la meilleure façon pour bien comprendre les mathématiques est de l’expliquer à une autre personne. Pour cela je te conseille d’aider des autres personnes dans leurs études. Même sur des sujets que tu penses qu’ils sont très faciles, tu vas découvert   quand tu répètes les notions du ce sujet que tu as beaucoup bénéficié et ça va t’aider dans votre étude.

Je suis Alaa Bou Kassem, je prépare un master en capes de mathématiques. Enseignant des maths depuis 2009, j'ai monté mon blog pour les élèves du cycle secondaire et toute  personne intéressée par les maths.                         N'hésitez pas à partager vos idées.